Математика је област која често изазива нашу интуицију, посебно када се бавимо концептима бесконачности и избора. Три кључна појма која се истичу у овом контексту су аксиом избора, принцип доброг уређења и парадокс Банаш-Тарског.
Ови концепти су дубоко повезани и имају значајне последице у теорији скупова и другим областима математике.
Аксиом избора
Аксиом избора је фундаментални принцип у теорији скупова који тврди да је за било коју колекцију непразних скупова могуће изабрати по један елемент из сваког скупа, чак и када не постоји експлицитно правило за тај избор.
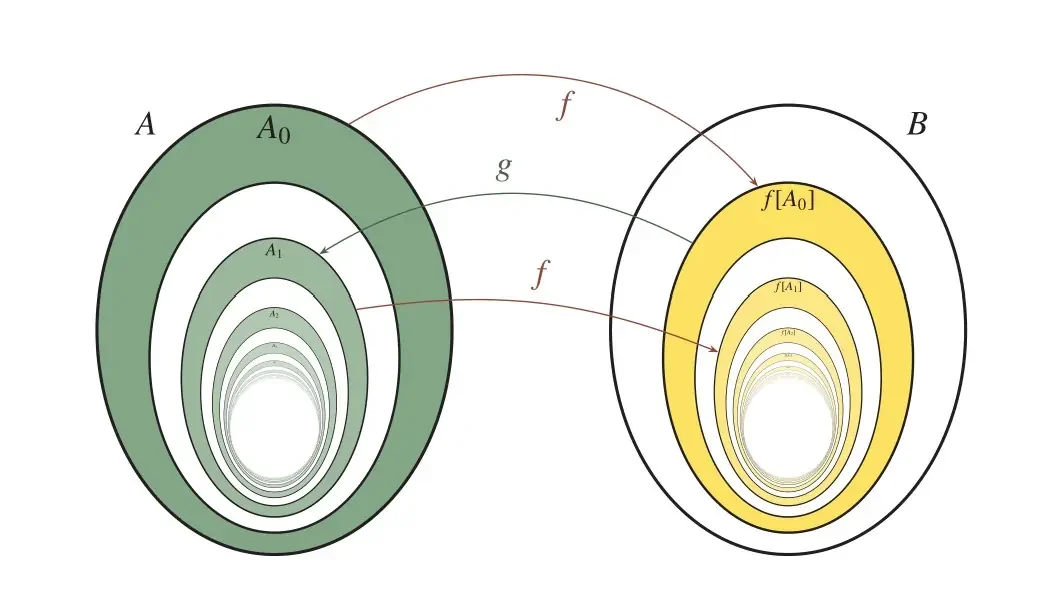
Формално, то значи да за сваку фамилију непразних скупова постоји функција избора која сваком скупу додељује један његов елемент. Овај аксиом је први пут формулисао немачки математичар Ернст Цермело 1904. године како би доказао теорему о добром уређењу.
Аксиом избора је контроверзан јер води до резултата који су контраинтуитивни. На пример, омогућава конструкцију скупова који немају Лебегову меру, што значи да им се не може придружити интуитивни појам запремине. Иако је аксиом избора широко прихваћен и користи се у многим гранама математике, постоје математичари који га оспоравају због његових неинтуитивних последица.
Принцип доброг уређења
Принцип доброг уређења тврди да се сваки скуп може добро уредити, што значи да постоји тотални редослед на скупу такав да свака непразна подскупина има најмањи елемент. Овај принцип је еквивалентан аксиому избора, што значи да ако прихватимо један од њих, можемо доказати други.
Цермело је користио аксиом избора да би доказао теорему о добром уређењу, што је изазвало значајне дебате у математичкој заједници почетком 20. века.
Парадокс Банаш-Тарског
Једна од најпознатијих и најзапањујућих последица аксиома избора је парадокс Банаш-Тарског. Овај парадокс тврди да је могуће разложити чврсту лопту у тродимензионалном простору на коначан број делова и затим их поново саставити на начин да се добију две идентичне копије оригиналне лопте.
Ови делови су веома компликовани и немогуће их је конструисати у физичком смислу, али њихово постојање је математички доказано уз помоћ аксиома избора.
Парадокс Банаш-Тарског показује како аксиом избора може довести до резултата који су у супротности са нашом интуицијом о запремини и мерењу. На пример, према овом парадоксу, могуће је узети лопту величине грашка и, након одређених математичких операција, добити лопту величине Сунца.
Ово наравно није физички изводљиво, али указује на сложеност и суптилност математичких концепата када се бавимо бесконачношћу и изборима.
Аксиом избора, принцип доброг уређења и парадокс Банаш-Тарског су кључни концепти у теорији скупова који истражују границе наше интуиције и разумевања бесконачности. Иако ови концепти могу деловати апстрактно и контраинтуитивно, они имају дубоке импликације у математици и помажу у обликовању нашег разумевања структуре и својстава скупова.